So-Bogus
A c++ sparse block matrix library aimed at Second Order cone problems
 All Classes Namespaces Functions Variables Typedefs Enumerations Enumerator Pages
Public Types | Public Member Functions | List of all members
bogus::LCPLaw< Scalar > Class Template Reference

LCP local solver that can be used within GaussSeidel and ProjectedGradient solvers. More...

#include <LCPLaw.hpp>

Public Types

enum  { dimension = 1 }
 
typedef LocalProblemTraits
< dimension, Scalar > 		Traits
 

Public Member Functions

 LCPLaw ()
 Constructor.
 
Scalar eval (const unsigned problemIndex, const typename Traits::Vector &x, const typename Traits::Vector &y) const
 
bool solveLocal (const unsigned problemIndex, const typename Traits::Matrix &A, const typename Traits::Vector &b, typename Traits::Vector &x, const Scalar scaling) const
 Solves the local problem. More...
 
void projectOnConstraint (const unsigned problemIndex, typename Traits::Vector &x) const
 Projects x on 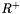$ R^+ $.
 
template<typename Segment >
void dualityCOV (const unsigned, const Segment &, typename Traits::Vector &s) const
 This NSLaw is always associated, so dualityCOV is null.
 

Detailed Description

template<typename Scalar>
class bogus::LCPLaw< Scalar >

LCP local solver that can be used within GaussSeidel and ProjectedGradient solvers.

For demonstration purposes. Since blocks are 1x1, other libraries are probably more suited.

Template Parameters
Scalarthe scalar type
Dimensionthe dimension of the blocks of the global matrix

Member Function Documentation

template<typename Scalar >
Scalar bogus::LCPLaw< Scalar >::eval ( const unsigned  problemIndex,
const typename Traits::Vector &  x,
const typename Traits::Vector &  y 
) const
Returns
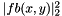$ \vert fb( x, y ) \vert^2_2 $, where fb is the scalar Fischer-Burmeister function
template<typename Scalar >
bool bogus::LCPLaw< Scalar >::solveLocal ( const unsigned  problemIndex,
const typename Traits::Matrix &  A,
const typename Traits::Vector &  b,
typename Traits::Vector &  x,
const Scalar  scaling 
) const

Solves the local problem.

$ 0 \leq x \perp a x + b \geq 0 $

The documentation for this class was generated from the following file: