Projected Gauss-Seidel iterative solver. More...

#include <GaussSeidel.hpp>

Inheritance diagram for bogus::GaussSeidel< BlockMatrixType >:

Public Types
typedef GaussSeidelBase < GaussSeidel, BlockMatrixType >	Base

typedef Base::GlobalProblemTraits	GlobalProblemTraits

typedef GlobalProblemTraits::Scalar	Scalar

typedef LocalProblemTraits < Base::BlockTraits::RowsPerBlock, Scalar >	BlockProblemTraits

typedef BlockMatrixTraits < BlockMatrixType >	BlockTraits

typedef Signal< unsigned, Scalar >	CallBackType

Public Member Functions
	GaussSeidel ()
	Default constructor – you will have to call setMatrix() before using the solve() function.

	GaussSeidel (const BlockObjectBase< BlockMatrixType > &matrix)
	Constructor with the system matrix.

GaussSeidel &	setMatrix (const BlockObjectBase< BlockMatrixType > &matrix)
	Sets the system matrix and initializes internal structures.

template<typename NSLaw , typename RhsT , typename ResT >
Scalar	solve (const NSLaw &law, const RhsT &b, ResT &x, bool tryZeroAsWell=true) const
	Finds an approximate solution for a constrained linear problem. More...

template<typename NSLaw , typename RhsT , typename ResT , typename LSDerived , typename HDerived >
Scalar	solveWithLinearConstraints (const NSLaw &law, const BlockObjectBase< LSDerived > &Cinv, const BlockObjectBase< HDerived > &H, const Scalar alpha, const RhsT &b, const RhsT &c, ResT &x, bool tryZeroAsWell=true, unsigned solveEvery=1) const

template<typename NSLaw , typename RhsT , typename ResT , typename WDerived >
Scalar	solveWithLinearConstraints (const NSLaw &law, const BlockObjectBase< WDerived > &W, const RhsT &b, ResT &x, bool tryZeroAsWell=true, unsigned solveEvery=1) const

Coloring &	coloring ()
	Access to the current Coloring. Will be reset whenever the matrix is changed. More...

void	setMaxThreads (unsigned maxThreads=0)
	Sets the maximum number of threads that the solver can use. More...

void	setAutoRegularization (Scalar maxRegul)
	Sets the auto-regularization (a.k.a. proximal point) coefficient. More...

void	setEvalEvery (unsigned evalEvery)
	Sets the number of iterations that should be performed between successive evaluations of the global error function. More...

void	setSkipTol (Scalar skipTol)
	Sets the minimum iteration step size under which local problems are temporarily frozen.

void	setSkipIters (unsigned skipIters)
	Sets the number of iterations for temporarily freezing local problems.

void	useInfinityNorm (bool useInfNorm)
	Sets whether the solver will use the infinity norm instead of the l1 one to compute the global residual from the local ones.

bool	usesInfinityNorm () const

Scalar	eval (const NSLaw &law, const ResT &y, const RhsT &x) const
	Eval the current global residual as a function of the local ones. More...

void	projectOnConstraints (const NSLaw &projector, VectorT &x) const
	Projects the variable `x` on the constraints defined by `projector`.

void	dualityCOV (const NSLaw &law, const RhsT &b, ResT &x) const
	Compute associated change of variable (see NSLaw)

Scalar	solve (const NSLaw &law, const RhsT &b, ResT &x) const

void	setMaxIters (unsigned maxIters)
	For iterative solvers: sets the maximum number of iterations.

unsigned	maxIters () const

void	setTol (Scalar tol)
	For iterative solvers: sets the solver tolerance.

Scalar	tol () const

CallBackType &	callback ()
	Callback hook; will be triggered every N iterations, depending on the solver. More...

const CallBackType &	callback () const

const BlockObjectBase < BlockMatrixType > &	matrix () const

Protected Types
typedef Base::Index	Index

typedef Base::BlockProblemTraits::Matrix	DiagonalBlockType

Protected Member Functions
void	updateLocalMatrices ()

template<typename NSLaw , typename RhsT , typename ResT >
void	innerLoop (bool parallelize, const NSLaw &law, const RhsT &b, std::vector< unsigned char > &skip, Scalar &ndxRef, ResT &x) const

const BlockMatrixBase < BlockMatrixType > &	explicitMatrix () const

const IterableBlockObject < BlockMatrixType > &	iterableMatrix () const

void	processLocalMatrices ()

Scalar	evalAndKeepBest (const NSLaw &law, const ResT &x, const typename GlobalProblemTraits::DynVector &y, typename GlobalProblemTraits::DynVector &x_best, Scalar &err_best) const

bool	tryZero (const NSLaw &law, const RhsT &b, ResT &x, typename GlobalProblemTraits::DynVector &x_best, Scalar &err_best) const

void	updateScalings ()

Protected Attributes
Coloring	m_coloring

ResizableSequenceContainer < DiagonalBlockType >::Type	m_localMatrices

GlobalProblemTraits::DynVector	m_regularization

unsigned	m_maxThreads
	See setMaxThreads(). Defaults to 0 .

unsigned	m_evalEvery
	See setEvalEvery(). Defaults to 25.

Scalar	m_skipTol
	See setSkipTol(). Defaults to 1.e-6.

unsigned	m_skipIters
	See setSkipIters() Defaults to 10.

Scalar	m_autoRegularization

GlobalProblemTraits::DynVector	m_scaling

bool	m_useInfinityNorm
	See useInfinityNorm(). Defaults to false.

const BlockObjectBase < BlockMatrixType > *	m_matrix
	Pointer to the matrix of the system.

unsigned	m_maxIters
	See setMaxIters()

Scalar	m_tol
	See setTol()

CallBackType	m_callback

Detailed Description

template<typename BlockMatrixType>
class bogus::GaussSeidel< BlockMatrixType >

Projected Gauss-Seidel iterative solver.

Works by taking into account only one block-row of the system at a time, and iterating several times over the whole set of rows several times until convergence has been achieved.

Each inner iteration of the algorithm will try to solve the local problem

$\left\{ \begin{array}{rcl} y_i^{k+1} &=& M_{i,i} x_i^{k+1} + b_i^{k} \\ &s.t.& law (x^{k+1},y^{k+1}) \end{array} \right.$

where k is the current global iteration, i the current row and

$b_i^{k} := b_i + \sum_{ j < i }{ M_{i,j}x_j^{k+1} } + \sum_{ j > i }{ M_{i,j}x_j^{k} }$

Member Function Documentation

template<typename BlockMatrixType >

CallBackType& bogus::BlockSolverBase< BlockMatrixType >::callback ( )

inherited

Callback hook; will be triggered every N iterations, depending on the solver.

Useful to monitor the convergence of the solver. Can be connected to a function that takes an unsigned and a Scalar as parameters. The first argument will be the current iteration number, and the second the current residual.

See Also: Signal< unsigned, Scalar >

template<typename BlockMatrixType>

Coloring& bogus::GaussSeidel< BlockMatrixType >::coloring ( )

Access to the current Coloring. Will be reset whenever the matrix is changed.

Determiniticy is achieved through the mean of contact coloring ; contacts that do not interact directly together can chare the same color, and all contacts within a given color can be solver in parallel

Scalar bogus::ConstrainedSolverBase< GaussSeidel< BlockMatrixType > , BlockMatrixType >::eval	(	const NSLaw &	law,
		const ResT &	y,
		const RhsT &	x
	)		const

inherited

Eval the current global residual as a function of the local ones.

y should be such that y = m_matrix * x + rhs

Returns

the current residual err defined as follow :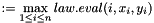

if m_useInfinityNorm is true, then err 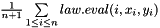$:= \max\limits_{1 \leq i \leq n } law.eval(i,x_i,y_i)$
else err := $\frac 1 {n+1} \sum\limits_{1 \leq i \leq n } law.eval(i,x_i,y_i)$

void bogus::GaussSeidelBase< GaussSeidel< BlockMatrixType > , BlockMatrixType >::setAutoRegularization ( Scalar maxRegul )

inherited

Sets the auto-regularization (a.k.a. proximal point) coefficient.

The regularization works by slightly altering the local problems, so at each iteration we try to solve

$\left\{ \begin{array}{rcl} y^{k+1} &=& ( M + \alpha I ) x^{k+1} - \alpha x^k + b^{k} \\ &s.t.& law (x^{k+1},y^{k+1}) \end{array} \right.$

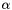where $\alpha$ is the regularization coefficient.

Note that as 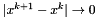$| x^{k+1} - x^{k} | \rightarrow 0$ when the algorithm converges, we are still trying to find a solution of the same global problem.

For under-determined problems, regularization might helps preventing x reaching problematically high values. Setting 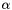$\alpha$ to a too big value will however degrade the convergence of the global algorithm.

Parameters

maxRegul If greater than zero, then positive terms will be added to the diagonal of the local matrices so that their minimal eigenvalue become greater than maxRegul.

void bogus::GaussSeidelBase< GaussSeidel< BlockMatrixType > , BlockMatrixType >::setEvalEvery ( unsigned evalEvery )

inherited

Sets the number of iterations that should be performed between successive evaluations of the global error function.

( Those evaluations require a full matrix/vector product, and are therfore quite costly )

void bogus::GaussSeidelBase< GaussSeidel< BlockMatrixType > , BlockMatrixType >::setMaxThreads ( unsigned maxThreads = 0 )

inherited

Sets the maximum number of threads that the solver can use.

If \p maxThreads is zero, then it will use the current OpenMP setting.

Warning: If multi-threading is enabled without coloring, the result will not be deterministic, as it will depends on the order in which threads solve contacts.

On the other hand, the algorithm will run much faster.

template<typename BlockMatrixType>

template<typename NSLaw , typename RhsT , typename ResT >

Scalar bogus::GaussSeidel< BlockMatrixType >::solve	(	const NSLaw &	law,
		const RhsT &	b,
		ResT &	x,
		bool	tryZeroAsWell = `true`
	)		const

Finds an approximate solution for a constrained linear problem.

Stops when the residual computed in eval() is below m_tol, of the number of iterations exceed m_maxIters

Implements Algorithm 1. from [2] to solve

$\left\{ \begin{array}{rcl} y &=& M x + b \\ &s.t.& law (x,y) \end{array} \right.$

Parameters

law	The (non-smooth) law that should define: An error function for the local problem A local solver for each row of the system ( e.g. 1 contact solver )

See Also: SOCLaw

Parameters

b	the const part of the right hand side
x	the unknown. Can be warm-started
tryZeroAsWell	If true, the algorithm will reset r to zero if that would result in a lower residual

template<typename BlockMatrixType>

template<typename NSLaw , typename RhsT , typename ResT , typename LSDerived , typename HDerived >

Scalar bogus::GaussSeidel< BlockMatrixType >::solveWithLinearConstraints	(	const NSLaw &	law,
		const BlockObjectBase< LSDerived > &	Cinv,
		const BlockObjectBase< HDerived > &	H,
		const Scalar	alpha,
		const RhsT &	b,
		const RhsT &	c,
		ResT &	x,
		bool	tryZeroAsWell = `true`,
		unsigned	solveEvery = `1`
	)		const

Solves

$\left\{ \begin{array}{rclll} y &=& M x &+ p &+ b \\ 0 &=& H^T x &+ \frac{1}{\alpha}C p &+ c \\ &s.t.& law (x,y) \end{array} \right.$

where Cinv is such that Cinv * x = 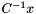$C^{-1} x$

Warning: Requires: m_evalEvery multiple of solveEvery ;

template<typename BlockMatrixType>

template<typename NSLaw , typename RhsT , typename ResT , typename WDerived >

Scalar bogus::GaussSeidel< BlockMatrixType >::solveWithLinearConstraints	(	const NSLaw &	law,
		const BlockObjectBase< WDerived > &	W,
		const RhsT &	b,
		ResT &	x,
		bool	tryZeroAsWell = `true`,
		unsigned	solveEvery = `1`
	)		const

Solves

$\left\{ \begin{array}{rcl} y &=& M x + W x + b \\ &s.t.& law (x,y) \end{array} \right.$

with W arbitrary linear operator ( matrix or expression )

Warning: Requires: m_evalEvery multiple of solveEvery ;

Member Data Documentation

Scalar bogus::GaussSeidelBase< GaussSeidel< BlockMatrixType > , BlockMatrixType >::m_autoRegularization

protectedinherited

See Also: setAutoRegularization(). Defaults to 0.

template<typename BlockMatrixType>

Coloring bogus::GaussSeidel< BlockMatrixType >::m_coloring

protected

See Also: coloring()

The documentation for this class was generated from the following file:

GaussSeidel.hpp

Public Types

Public Member Functions

Protected Types

Protected Member Functions

Protected Attributes

Detailed Description

template<typename BlockMatrixType> class bogus::GaussSeidel< BlockMatrixType >

Member Function Documentation

Member Data Documentation

template<typename BlockMatrixType>
class bogus::GaussSeidel< BlockMatrixType >