Non-smooth laws based on Second Order Cone complementarity. To be used within as the first argument to GaussSeidel::solve(). More...

#include <SOCLaw.hpp>

Public Types
enum	{ dimension = Dimension }

typedef LocalProblemTraits < Dimension, Scalar >	Traits

Public Member Functions
	SOCLaw (const unsigned n, const double *mu)
	Constructor. More...

Scalar	eval (const unsigned problemIndex, const typename Traits::Vector &x, const typename Traits::Vector &y) const

bool	solveLocal (const unsigned problemIndex, const typename Traits::Matrix &A, const typename Traits::Vector &b, typename Traits::Vector &x, const Scalar scaling) const
	Solves the local problem. More...

void	projectOnConstraint (const unsigned problemIndex, typename Traits::Vector &x) const
	Projects x on 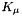$K_{ \mu }$ .

template<typename Segment >
void	dualityCOV (const unsigned problemIndex, const Segment &y, typename Traits::Vector &s) const
	Computes the change of variable `s(y)` so that (x, y+s(y)) obeys an associated law. More...

Detailed Description

Non-smooth laws based on Second Order Cone complementarity. To be used within as the first argument to GaussSeidel::solve().

Template Parameters

Dimension	the dimension of the local problem. Specializations exist form dimension 2 and 3.
Scalar	the scalar type
DeSaxceCOV	Whether to perform the [3] change of variable when solving the local problem. Should be `true` for modeling Coulomb friction, or `false` for standard SOC complementarity.

Template Parameters

Strat local_soc_solver::Strategy for solving the local problems. Unavailable for dimensions other than 2 and 3.

Constructor & Destructor Documentation

template<DenseIndexType Dimension, typename Scalar , bool DeSaxceCOV, local_soc_solver::Strategy Strat = local_soc_solver::RevHybrid>

bogus::SOCLaw< Dimension, Scalar, DeSaxceCOV, Strat >::SOCLaw	(	const unsigned	n,
		const double *	mu
	)

Constructor.

Parameters

n	the size of the global problem ( number of contacts )
mu	array containing the apertures of each second order cone ( friction coefficients )

template<DenseIndexType Dimension, typename Scalar , bool DeSaxceCOV, local_soc_solver::Strategy Strat = local_soc_solver::RevHybrid>

template<typename Segment >

void bogus::SOCLaw< Dimension, Scalar, DeSaxceCOV, Strat >::dualityCOV	(	const unsigned	problemIndex,
		const Segment &	y,
		typename Traits::Vector &	s
	)		const

Computes the change of variable s(y) so that (x, y+s(y)) obeys an associated law.

ie 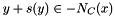$y + s(y) \in - N_C(x)$ . Here C = K_{mu}, and if

Template Parameters

DeSaxceCOV is true, 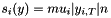$s_i(y) = mu_i |y_{i,T}| n$

template<DenseIndexType Dimension, typename Scalar , bool DeSaxceCOV, local_soc_solver::Strategy Strat = local_soc_solver::RevHybrid>

Scalar bogus::SOCLaw< Dimension, Scalar, DeSaxceCOV, Strat >::eval	(	const unsigned	problemIndex,
		const typename Traits::Vector &	x,
		const typename Traits::Vector &	y
	)		const

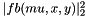Returns: $\vert fb( mu, x, y ) \vert^2_2$ , where fb is the SOC Fischer-Burmeister function

template<DenseIndexType Dimension, typename Scalar , bool DeSaxceCOV, local_soc_solver::Strategy Strat = local_soc_solver::RevHybrid>

bool bogus::SOCLaw< Dimension, Scalar, DeSaxceCOV, Strat >::solveLocal	(	const unsigned	problemIndex,
		const typename Traits::Matrix &	A,
		const typename Traits::Vector &	b,
		typename Traits::Vector &	x,
		const Scalar	scaling
	)		const

Solves the local problem.

$\left\{ \begin{array}{rcl} y &=& \mathrm{ <DS> } \left( A x + b \right ) \\ K_{ \frac 1 \mu } \ni y & \perp & x \in K_{ \mu } \end{array} \right.$

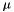where $\mu$ is m_mu[problemIndex] and <DS> is the optional De Saxce change of variable.

That is, if DeSaxceCOV is false then <DS> is the identity function, otherwise

$\mathrm{ <DS> }( x ) := x + \mu \vert x_T \vert \left( 1, 0, ... \right)^{\top}$

Parameters

scaling Used as a scaling factor for x when calculating the error function

The documentation for this class was generated from the following files: