So-Bogus
A c++ sparse block matrix library aimed at Second Order cone problems
 All Classes Namespaces Functions Variables Typedefs Enumerations Enumerator Pages
Classes | Public Types | Public Member Functions | Protected Member Functions | Protected Attributes | List of all members
bogus::MecheFrictionProblem Class Reference

Classes

struct  Options
 

Public Types

enum  Algorithm {
  GaussSeidel = 0, ProjectedGradient = 1, MatrixFreeGaussSeidel, ADMM,
  DualAMA
}
 

Public Member Functions

void fromPrimal (unsigned int NObj, const unsigned int *ndof, const double *const *MassMat, const double *f_in, unsigned int n_in, const double *mu_in, const double *E_in, const double *w_in, const int *const ObjA, const int *const ObjB, const double *const HA[], const double *const HB[])
 Allocates and sets up the primal friction problem. More...
 
double solve (double *r, double *v, bool staticProblem, double problemRegularization, const Options &options)
 Solves the friction problem. More...
 
double solve (double *r, double *v, int maxThreads=0, double tol=0., unsigned maxIters=0, bool staticProblem=false, double regularization=0., bool useInfinityNorm=false, bool useProjectedGradient=false, unsigned cadouxIters=0)
 Solves the friction problem (old interface) More...
 
void computeDual (double regularization)
 Computes the dual from the primal.
 
void reset ()
 Cleams up the problem, then allocates a new PrimalFrictionProblem and make m_primal point to it.
 
unsigned nDegreesOfFreedom () const
 
unsigned nContacts () const
 
void setOutStream (std::ostream *out)
 Sets the standard output stream ( out can be NULL to remove all output )
 
Signal< unsigned, double,
double > & 		callback ()
 Signal< interationNumber, error, elapsedTime > that will be triggered every few iterations.
 
bool dumpToFile (const char *fileName, const double *r0=(static_cast< const double * >(0))) const
 Dumps the current primal() to fileName. More...
 
bool fromFile (const char *fileName, double *&r0)
 Loads the primal from a previously saved problem file. More...
 
void ackCurrentResidual (unsigned GSIter, double err)
 
const PrimalFrictionProblem< 3u > & primal () const
 
const DualFrictionProblem< 3u > & dual () const
 
PrimalFrictionProblem< 3u > & primal ()
 
DualFrictionProblem< 3u > & dual ()
 
double * f ()
 
double * w ()
 
double * mu ()
 
double lastSolveTime () const
 Time spent in last solver call. In seconds.
 

Protected Member Functions

void destroy ()
 

Protected Attributes

PrimalFrictionProblem< 3u > * m_primal
 
DualFrictionProblem< 3u > * m_dual
 
double m_lastSolveTime
 
Signal< unsigned, double, double > m_callback
 
Timer m_timer
 

Member Function Documentation

bool bogus::MecheFrictionProblem::dumpToFile ( const char *  fileName,
const double *  r0 = (static_cast< const double *>(0)) 
) const

Dumps the current primal() to fileName.

Parameters
r0The initial guess that shouls be saved with the problem, or NULL
bool bogus::MecheFrictionProblem::fromFile ( const char *  fileName,
double *&  r0 
)

Loads the primal from a previously saved problem file.

Parameters
r0Will be set to ploint to a newly allocated array containing the initial guess, if such one was saved with the problem. Will have to be manually freed by the caller using the delete[] operator.
void bogus::MecheFrictionProblem::fromPrimal ( unsigned int  NObj,
const unsigned int *  ndof,
const double *const *  MassMat,
const double *  f_in,
unsigned int  n_in,
const double *  mu_in,
const double *  E_in,
const double *  w_in,
const int *const  ObjA,
const int *const  ObjB,
const double *const  HA[],
const double *const  HB[] 
)

Allocates and sets up the primal friction problem.

Warning
copies the contents of the matrices M, E and H ! Manually constructing a PrimalFrictionProblem would be more efficient
Parameters
NObjnumber of subsystems
ndofarray of size NObj, the number of degree of freedom of each subsystem
MassMatarray of pointers to the mass matrix of each subsystem
f_inthe constant term in 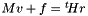$ M v + f= {}^t \! H r $
n_innumber of contact points
mu_inarray of size n giving the friction coeffs
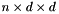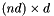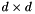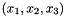E_inarray of size $ n \times d \times d $ giving the n normals followed by the n tangent vectors (and by again n tangent vectors if d is 3). Said otherwise, E is a $ (nd) \times d $ matrix, stored column-major, formed by n blocks of size $ d \times d $ with each block being an orthogonal matrix (the transition matrix from the world space coordinates $ (x_1, x_2, x_3) $ to the local coordinates $ (x_N, x_{T1}, x_{T2}) $
w_inarray of size nd, the constant term in 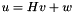$ u = H v + w $
ObjAarray of size n, the first object involved in the i-th contact (must be an internal object) (counted from 0)
ObjBarray of size n, the second object involved in the i-th contact (-1 for an external object) (counted from 0)
HAarray of size n, containing pointers to a dense, colum-major matrix of size d*ndof[ObjA[i]] corresponding to the H-matrix of ObjA[i]
HBarray of size n, containing pointers to a dense, colum-major matrix of size d*ndof[ObjA[i]] corresponding to the H-matrix of ObjB[i] (NULL for an external object)
double bogus::MecheFrictionProblem::solve ( double *  r,
double *  v,
bool  staticProblem,
double  problemRegularization,
const Options &  options 
)

Solves the friction problem.

Parameters
rlength nd : initialization for r (in world space coordinates) + used to return computed r
vlength m: to return computed v ( or NULL if not needed )
staticProblemIf true, do not use DeSaxce change of variable
problemRegularizationAmount to add on the diagonal of the Delassus operator
optionsSolver options
double bogus::MecheFrictionProblem::solve ( double *  r,
double *  v,
int  maxThreads = 0,
double  tol = 0.,
unsigned  maxIters = 0,
bool  staticProblem = false,
double  regularization = 0.,
bool  useInfinityNorm = false,
bool  useProjectedGradient = false,
unsigned  cadouxIters = 0 
)

Solves the friction problem (old interface)

Parameters
rlength nd : initialization for r (in world space coordinates) + used to return computed r
vlength m: to return computed v ( or NULL if not needed )
maxThreadsMaximum number of threads that the GS will use. If 0, use OpenMP default. If > 1, enable coloring to ensure deterministicity
tolGauss-Seidel tolerance. 0. means GS's default
maxItersMax number of iterations. 0 means GS's default
staticProblemIf true, do not use DeSaxce change of variable
regularizationCoefficient to add to the diagonal of static problems / GS regularization coefficient for friction problems
useInfinityNormWhether to use the infinity norm to evaluate the residual of the friction problem,
useProjectedGradient0 = GS, 1 = PG, 2 = ADMM, 3 = DualAMA.
cadouxItersIf staticProblem is false and cadouxIters is greater than zero, use the Cadoux algorithm to solve the friction problem.
The documentation for this class was generated from the following files: