So-Bogus
A c++ sparse block matrix library aimed at Second Order cone problems
 All Classes Namespaces Functions Variables Typedefs Enumerations Enumerator Pages
Public Types | Public Member Functions | Public Attributes | List of all members
bogus::DualFrictionProblem< Dimension > Struct Template Reference

Dual representation of a Coulomb friction problem, with explicit Delassus operator. More...

#include <FrictionProblem.hpp>

Public Types

typedef SparseBlockMatrix
< Eigen::Matrix< double,
Dimension, Dimension,
Eigen::RowMajor >, SYMMETRIC > 		WType
 
typedef GaussSeidel< WType > GaussSeidelType
 
typedef ProjectedGradient< WType > ProjectedGradientType
 
typedef SOCLaw< Dimension,
double, true > 		CoulombLawType
 
typedef SOCLaw< Dimension,
double, false > 		SOCLawType
 
typedef Signal< unsigned, double > SignalType
 

Public Member Functions

void computeFrom (const PrimalFrictionProblem< Dimension > &primal)
 Computes this DualFrictionProblem from the given primal. More...
 
double solveWith (GaussSeidelType &gs, double *r, const bool staticProblem=false) const
 Solves this problem. More...
 
double solveWith (ProjectedGradientType &pg, double *r) const
 
double evalWith (const GaussSeidelType &gs, const double *r, const bool staticProblem=false) const
 Evaluate a residual using the GS's error function. More...
 
double evalWith (const ProjectedGradientType &gs, const double *r) const
 
double solveCadoux (GaussSeidelType &gs, double *r, const unsigned fpIterations, const SignalType *callback=(static_cast< const SignalType * >(0))) const
 Solves this problem using the Cadoux algorithm ( with fixed-point iteration ) More...
 
double solveCadoux (ProjectedGradientType &pg, double *r, const unsigned fpIterations, const SignalType *callback=(static_cast< const SignalType * >(0))) const
 
double solveCadouxVel (GaussSeidelType &gs, double *u, const unsigned fpIterations, const SignalType *callback=(static_cast< const SignalType * >(0))) const
 Idem as solveCadoux, but interpreting the problem as r = Wu + b.
 
double solveCadouxVel (ProjectedGradientType &pg, double *u, const unsigned fpIterations, const SignalType *callback=(static_cast< const SignalType * >(0))) const
 
void applyPermutation (const std::vector< std::size_t > &permutation)
 Apply a permutation on the contact indices. More...
 
void undoPermutation ()
 
bool permuted () const
 
const std::vector< std::size_t > & permutation () const
 
const std::vector< std::size_t > & invPermutation () const
 

Public Attributes

WType W
 W – Delassus operator.
 
Eigen::VectorXd b
 Rhs ( such that u = Wr + b )
 
Eigen::VectorXd mu
 Coulomb friction coefficients.
 

Detailed Description

template<unsigned Dimension>
struct bogus::DualFrictionProblem< Dimension >

Dual representation of a Coulomb friction problem, with explicit Delassus operator.

u = W r + b such that u and r satisfy CoulombLaw(mu) or SOCLaw(mu), where W is a symmetric, positive semi-definite matrix with 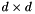$ d \times d $ blocks, u are the relative velocities and r are the contact forces. May be constructed from a PrimalFrictionProblem, or by directly initializing each data member to accomodate problems with different mass matrix structures. See also Constrained Iterative Solvers .

Member Function Documentation

template<unsigned Dimension>
void bogus::DualFrictionProblem< Dimension >::applyPermutation ( const std::vector< std::size_t > &  permutation)

Apply a permutation on the contact indices.

Useful for achieving better memory locality when using the Coloring functionality of the GaussSeidel algorithm.

See Also
Coloring
Warning
To use the permutation releated functions, all the blocks have to have the same size
template<unsigned Dimension>
void bogus::DualFrictionProblem< Dimension >::computeFrom ( const PrimalFrictionProblem< Dimension > &  primal)

Computes this DualFrictionProblem from the given primal.

Warning
Assumes MInv has been computed
template<unsigned Dimension>
double bogus::DualFrictionProblem< Dimension >::evalWith ( const GaussSeidelType &  gs,
const double *  r,
const bool  staticProblem = false 
) const

Evaluate a residual using the GS's error function.

Parameters
gsThe GaussSeidel< WType > solver to use
rBoth the current force
staticProblemIf true, eval this problem as a SOCQP instead of a Coulomb Friction problem
Returns
the error as returned by the GaussSeidel::eval() function
template<unsigned Dimension>
double bogus::DualFrictionProblem< Dimension >::solveCadoux ( GaussSeidelType &  gs,
double *  r,
const unsigned  fpIterations,
const SignalType *  callback = (static_cast< const SignalType *>(0)) 
) const

Solves this problem using the Cadoux algorithm ( with fixed-point iteration )

See [1]

Parameters
gsThe GaussSeidel< WType > solver to use
rBoth the initial guess and the result
fpIterationsNumber of fixed-point iterations
callback0, or a pointer to a user-defined function that takes ( unsigned iteration, double residual ) as arguments
Returns
the error as returned by the GaussSeidel::solve() function
template<unsigned Dimension>
double bogus::DualFrictionProblem< Dimension >::solveWith ( GaussSeidelType &  gs,
double *  r,
const bool  staticProblem = false 
) const

Solves this problem.

Parameters
gsThe GaussSeidel< WType > solver to use
rBoth the initial guess and the result
staticProblemIf true, solve this problem as a SOCQP instead of a Coulomb Friction problem
Returns
the error as returned by the GaussSeidel::solve() function
The documentation for this struct was generated from the following files: