|
So-Bogus
A c++ sparse block matrix library aimed at Second Order cone problems
|
|
So-Bogus
A c++ sparse block matrix library aimed at Second Order cone problems
|
To use this library,
The BlockSolvers module is a collection of solvers operating on Block matrices.
At the moment, those solvers are:
A few Krylov methods are available through the Krylov class, as well as some naive preconditioners. For the full list of available solvers, see the krylov::Method enum or the krylov::solvers namespace.
Here is some code solving a very simple system without preconditioning:
If we wanted to use a preconditioner
... or sparse matrices
Iterative linear solvers may also be used in a matrix-free version – that is, without explictely computing the system matrix. Suppose that we want to solve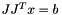 
, this can be done as
Alternatively, a Krylov object may be converted to a particular method-object which inherits from LinearSolverBase. This means it can be used as a BlockType of a SparseBlockMatrix, and can offer more configuration options, such as setting the 'restart' option for the krylov::GMRES method.
The main feature of the BlockSolvers module is providing solvers for a specific class of nonsmooth problems, which includes
More specifically, we are concerned with problems that can be expressed as
![\[ \begin{array}{rcl} y &=& M x + b \\ y_i + s_i(y_i) & \in &- \mathcal{N}_{C_i}( x_i ) \quad \forall i. \end{array} \]](form_50.png)
where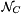 
denotes the normal cone to the set C. The dimensions of the sets 
should correspond to that of the blocks of rows of M. If 
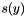is zero, we retrieve the optimality conditions of the quadratic minimization problem
![\[ \min_{x \in C} \frac 1 2 x^T M x + x^T b \]](form_47.png)
Depending on the solver, M may need to be an explicit matrix (i.e. an instance of BlockMatrixBase), or simply an expression (for instance, a Product, NarySum, or a LinearSolverBase ).
The definition of the constraint set C and of the translation term s(y) is done by passing a NSLaw to the solve() function of the solvers. The NSLaw should conform to a specific interface, and provide at least
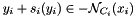at the i^th blockSupplemental methods may need to be provided by the NSLaw depending on the solver chosen. See LCPLaw, SOCLaw or PyramidLaw for examples of the interfaces that should be provided by a NSLaw.
Implementations of Constrained Iterative Solvers include Projected Gauss Seidel (GaussSeidel, ProductGaussSeidel) and Projected Gradient (ProjectedGradient) , as well as the experimental ADMM and DualAMA classes.
Constrained linear systems can be solved using the GaussSeidel or ProductGaussSeidel classes, as long as a NSLaw defining a corresponding NSLaw::solveLocal() function is available. SOCLaw, from the Second Order module, is an example of such NSlaw.
Example code for 3D Coulomb friction (requires the Second Order module):
System with supplemental linear equality constraints may be solved with the GaussSeidel::solveWithLinearConstraints function.
The ProductGaussSeidel class is useful when explicitely computing the matrix W would be expensive, but the product MInv * H' is quite sparse (that is, when updating a force component does not impact too many degrees of freedom). When Minv is the identity matrix, the above example can then be modified as
When Minv is not the idenity matrix, one may use
The ProjectedGradient class may be used to compute the solution of the quadratic minimization problem
using a variant of the Projected Gradient or Projected Gradient Descent algorithms. Its interface is very similar to that of the above GaussSeidel. A few variants of the algorithm, such as the Nesterov [7] acceleration, are implemented; they can be selected using the ProjectedGradient::setDefaultVariant() method or using a template parameter. See projected_gradient::Variant for more information.
Once again, this algorithm can be used in a matrix-free fashion
The NSLaw passed to the ProjectedGradient::solve() method should define a projectOnConstraint() function that computes the orthogonal projection onto the constraint set C.
1.8.5 
