Introduction

The goal of this module is to make arithmetic expressions involving sparse block matrices trivial to express, without sacrificing performance. For instance, we will be able to compute the regularized Delassus operator, 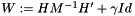$W := H M^{-1} H' + \gamma Id$ simply by writing

W = H * ( MInv * H.transpose() ) + gamma * Id ;

where MInv is a block diagonal matrix containing LDLT factorizations of the diagonal blocks of M. The evaluation will be somewhat lazy – which means that it will try to use as little as possible temporary storage – and will take advantage of parallel architectures – provided OpenMP support is enabled, see Configuration.

Basics

To use this library,

#include <bogus/Core/Block.impl.hpp>
// If you need serialization capabilities
#include <bogus/Core/Block.io.hpp>

The main user-fronting class of this library is SparseBlockMatrix, even if most of its methods are actually implemented by its parent, SparseBlockMatrixBase. Alternatively, the MappedSparseBlockMatrix class allows an externally constructed sparse block matrix to be used inside bogus expressions.

SparseBlockMatrix and MappedSparseBlockMatrix are templated with a block type, and an optional set of flags. The library has been written to mainly accept Eigen dense and sparse matrices as block types, though little effort is required to make it compatible with other types. Additionally, scalar types ( such as double, float or int ) are supported out of the box, as well as LU and LDLT factorizations of Eigen matrices.

The possible values for the flags are a combination of:

flags::COL_MAJOR
flags::SYMMETRIC
flags::UNCOMPRESSED ( except for MappedSparseBlockMatrix which maps to a compressed index format )

Creating a SparseBlockMatrix

Three steps are necessary to create a block sparse matrix:

Define the block dimensions using SparseBlockMatrixBase::setRows() and SparseBlockMatrixBase::setCols()
Optionally pre-allocate the necessary memory using SparseBlockMatrixBase::reserve()
Insert the non-zeros block using SparseBlockMatrixBase::insertBack(), SparseBlockMatrixBase::insert() or one of their variations
Call SparseBlockMatrixBase::finalize() . Really. This would have been a legitimate use for the late HTML blink tag.

Example: Creating a block-diagonal matrix

//  Creates the following matrix:
//
//  1 1 0 0
//  1 1 0 0
//  1 1 0 0
//  0 0 1 1
//  0 0 1 1
//
int rowsPerBlock[2] = { 3, 2 } ;
bogus::SparseBlockMatrix< Eigen::MatrixXd > sbm ;
sbm.setRows( 2, rowsPerBlock ) ; // 2 block-rows which each have a number of rows given by rowsPerBlock
sbm.setCols( 2, 2 ) ; // 2 block-columns which all have 2 columns
// Insert the diagonal blocks
sbm.insertBackAndResize( 0, 0 ).setOnes() ;
sbm.insertBackAndResize( 1, 1 ).setOnes() ;
sbm.finalize() ; // Compulsory !

Note that you don't have to specify the block contents before the call to SparseBlockMatrixBase::finalize(). Furthermore, if you don't want the resize() method to be called at insert time, you can just use SparseBlockMatrixBase::insertBack(). The following code would work just as well, despite the increased verbosity:

bogus::SparseBlockMatrix< Eigen::MatrixXd > sbm ;
// Insert the diagonal blocks
sbm.insertBack(0,0) ;
sbm.insertBack(1,1) ;
sbm.finalize() ; // Compulsory !
sbm.block(0,0) = Eigen::MatrixXd::Ones( 3, 2 ) ;
sbm.diagonal(1) = Eigen::MatrixXd::Ones( 2, 2 ) ;

The SparseBlockMatrixBase::insertBack() insertion method requires the blocks to be inserted in order. That is, for a row-major block matrix, filling the rows in increasing order, and filling each row with stricly increasing column indices.

Alternatively, for matrices with an uncompressed index, the SparseBlockMatrixBase::insert() method may be used. In this case, there are no restrictions on the order in which blocks are inserted. However, this is at the cost of poorer performance. Please refere to those methods documentation for more details.

Creating a MappedSparseBlockMatrix

MappedSparseBlockMatrix are const references to either

another SparseBlockMatrixBase object that uses a compressed index
an external matrix in a BSR-like format ( e.g. it can handle column-major matrices as well )

For instance, mapping to a SparseBlockMatrix

bogus::SparseBlockMatrix< Eigen::Matrix3d > source ;
//[...]  Fill source
bogus::MappedSparseBlockMatrix< Eigen::Matrix3d > map ;
map.mapTo( source ) ;
// can also be done using the BSR interface
map.cloneDimensions( source ) ;
map.mapTo( source.nBlocks(),
    source.data(),
    source.majorIndex().outerIndexPtr(),
    source.majorIndex().innerIndexPtr()
    );

in the previous example, note that the call to SparseBlockMatrixBase::cloneDimensions() could be replaced by calls to SparseBlockMatrixBase::setRows() and SparseBlockMatrixBase::setCols().

Reading the contents of a SparseBlockMatrix

Iterators over the inner dimension of a SparseBlockMatrix can be constructed using the SparseBlockMatrixBase::innerIterator() method. For instance, the contents of a row-major matrix can be read as follow

typedef bogus::SparseBlockMatrix< Eigen::MatrixXd > SBM ;
SBM sbm ;
//...
for( int row = 0 ; row < sbm.rowsOfBlocks() ; ++ row ) {
    for( SBM::InnerIterator it ( sbm.innerIterator( row ) ) ; it ; ++it ) {
        std::cout << "Block at (" << row << ", " << it.inner() << ") is \n "
                  << sbm.block( it.ptr() ) << "\n" ;
    }
}

Using a SparseBlockMatrix (or a MappedSparseBlockMatrix)

Currently, the following operations are supported:

Most of those operations can be done using the standard C++ operators, in a lazy way – the resulting matrix will only be computed when assigned to another BlockMatrix. Since it is immutbale, a MappedSparseBlockMatrix can only be used in the righ-hand-side of those operations, never as a left-hand-side.

Warning: The operations should be able to be composed in an arbitrary way, but in pratice there are a few Limitations.

Assignment

Any SparseBlockmatrix can be assigned to another one, as long as their block types are compatible.

bogus::SparseBlockMatrix< Eigen::Matrix3d, bogus::UNCOMPRESSED  > sbm ;
// Fill sbm
// ...
// Assignment
bogus::SparseBlockMatrix< Eigen::MatrixXd, bogus::COL_MAJOR >
  sbm2 = sbm ;

Coefficient-wise scaling

The multiplication of each block of a SparseBlockMatrix with a scalar can be conveniently done using the SparseBlockMatrixBase::scale() method or the '*=' and '/=' operators.

Transpose

Transposing a block matrix can be done with the SparseBlockMatrixBase::transpose() method. Note that this method does not do any work; it can only be used as the right hand side of an affectation operation, or inside an arithmetic operation ( see below )

Block Matrix/Block Matrix addition

Two block matrix can be added together using the standard '+' operator, provided they have the same block structure ( that is, their rows and columns of blocks must have similar dimensions ). This operator does no do any work, but just returns an Addition expression which will be evaluated when it is assigned to another SparseBlockMatrix.

Alternatively, the SparseBlockMatrixBase::add method provides a ?axpy-like interface which allows on-the-fly scaling of the right-hand-side. '-', '+=' and '-=' are also defined.

Examples

bogus::SparseBlockMatrix< Eigen::MatrixXd > sbm1 ;
// [...] fill sbm1
bogus::SparseBlockMatrix< Eigen::MatrixXd, bogus::SYMMETRIC > sbm2 ;
sbm2 = sbm1 + sbm1.transpose() ;
sbm1 -= sbm2 ;
sbm1.add< false >( sbm2, .5 ) ;

Block Matrix/Dense Vector multiplication

Multiplication with a Eigen dense vector ( or matrix ) can ben done using simply the standard '*' operator, or using the BlockMatrixBase::multiply() method for more flexibility ( BLAS ??mv-like ) and control over temporary memory allocation.

Some examples

Eigen::VectorXd res  = sbm * Eigen::VectorXd::Ones( n ) ;
Eigen::VectorXd res2 = sbm.transpose() * Eigen::VectorXd::Map( data, n )
sbm.multiply< true >( res2, res, -1, 1 ) ; // res -= sbm.transpose() * res2

Note: When using the * operator, the result of the operation will be evaluated lazily, that is not until it is assigned to another vector or evaluated as part of a larger expression. However, for aliasing safety reasons and consistency with the Eigen library, the matrix-vector product may sometimes be unecessarily be evaluated inside a temporary. You can change this behavior using the noalias() operator of Eigen lvalues:
Eigen::VectorXd rhs, res ;

// Equivalent to Eigen::VectorXd tmp = sbm*rhs ; res += sbm ;

res += sbm * rhs ;

// Equivalent to sbm.multiply< false >( rhs, res, 1, 1 ) ;

res.noalias() += sbm * rhs ;

Block Matrix/Block Matrix multiplication

Two SparseBlockMatrix can me multiplied provided the dimensions of their blocks are compatible, using the standard '*' operator. The return type of this operator is a Product expression, which in itself does not perform any computation; the proper multiplication will only be done when it is assigned to another SparseBlockMatrix.

bogus::SparseBlockMatrix< GradBlockT > H ;
// [...] Fill H
bogus::SparseBlockMatrix< Eigen::Matrix3d, bogus::SYMMETRIC > W = H * H.transpose() ;

Expressions

bogus uses lazy evaluation, and as such does not evaluate operations between matrices immediately, but stores them inside expression templates. While these expressions are transparently resolved at assignment time, and therefore should not generally matter to the end-user, they may be useful for the definition of matrix-free iterative solvers (see e.g. Iterative Linear Solvers).

bogus defines two unary operations, Transpose and Scaling, and two binary operations, Product and Addition. For instance,

Addition< Scaling<AType>, Product< BType, Transpose<CType> > > expr = 3*A + B*C.transpose() ;

In certain situations, one may not know at compile time the number of operations that define an expression. For such scenarios, bogus defines the NarySum expression. For instance, if we want to use to use the expression 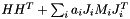$H H^T + \sum_i{ a_i J_i M_i J_i^T }$ as a system matrix, we can do

// Common type for each of the sum's operands
typedef bogus::Product< JType,
                  bogus::Product< MType, bogus::Transpose< JType > > >
                  JMJtProd ;
// Construct n-ary sum expression
// The (common) number of rows and columns of the operands has to be provided beforehand, in order to allow empty sum expressions
bogus::NarySum< JMJtProd > sum( nRows, nCols ) ;
for( unsigned i = 0 ; i < Jmatrices.size() ; ++i ) {
    const JType &J = Jmatrices[i] ;
    sum += a[i] * ( J * ( Mmatrices[i] * J.transpose() ) );
}
  
// Construct global expression
typedef bogus::Product< HType, bogus::Transpose< HType > > HHtProd ;
typedef bogus::Addition< HHtProd, bogus::NarySum< JMJtProd > > Expr ;
  
const Expr W = H * H.transpose() + sum ;
// Use the expression inside a linear solver
bogus::Krylov<Expr>(W).solve(b,x) ;

Limitations

As a rule of thumb, these limitations can be circumvented by explicitely assigning the result of each operation to a temporary object.

Aliasing

For performance reasons, operations on SparseBlockMatrix should not be assumed to be aliasing-safe. This is especially true for matrix-vector multiplication using directly BlockMatrixBase::multiply() ( rhs and res should not alias ), and matrix-matrix addition ( the matrix that is being assigned to should not appear anywhere but as the left-most operand ).

Type deduction

In some cases bogus will not be able to deduce the correct return type for an operation. This can happen for matrix-matrix products that have to be evaluated as a part of a larger arithmetic expressions, and which involve "unusual" block types. If such an error occurs, just assign the offending product to a temporary SparseBlockMatrix.

Performance

bogus will not necessarily choose the most optimized type for the evaluation of temporary expressions. For example, it might choose a row-major matrix when a column-major one would be more approriate, or fail to notice that H * H.transpose() should use symmetric storage.

Explicit parenthesisation will also help performance. Otherwise, bogus may perform matrix-matrix products in an inefficient order, or allocate unnecessary temporary matrices.

Other useful objects

Matrix-like objects

The Zero class is a useful placeholder for matrix arguments that are not always useful. For instance, in the GaussSeidel solver, problems with and without linear constraints use the same code; in the latter case, the constraint matrix is represented with the Zero class.

CompoundBlockMatrix is a utility class representing the concatenation of two objects, which may have different block types.

Table of Contents