So-Bogus
A c++ sparse block matrix library aimed at Second Order cone problems
 All Classes Namespaces Functions Variables Typedefs Enumerations Enumerator Pages
Public Types | Public Member Functions | Public Attributes | List of all members
bogus::PrimalFrictionProblem< Dimension > Struct Template Reference

Primal Coulomb friction problem for a block-diagonal mass matrix M with dense blocks. More...

#include <FrictionProblem.hpp>

Public Types

typedef SparseBlockMatrix
< Eigen::MatrixXd > 		MType
 
typedef Eigen::Matrix< double,
Dimension, Eigen::Dynamic > 		HBlock
 
typedef SparseBlockMatrix
< HBlock, UNCOMPRESSED > 		HType
 
typedef SparseBlockMatrix< LU
< Eigen::MatrixBase
< Eigen::MatrixXd > > > 		MInvType
 M^-1.
 
typedef ADMM< HType > ADMMType
 
typedef DualAMA< HType > DualAMAType
 
typedef ProductGaussSeidel
< HType, MInvType, true > 		ProductGaussSeidelType
 

Public Member Functions

void computeMInv ()
 
double solveWith (ProductGaussSeidelType &pgs, double *r, const bool staticProblem=false) const
 Matrix-free Gauss-Seidel solver. More...
 
double solveWith (ADMMType &admm, double lambda, double *v, double *r) const
 ADMM (Alternating Direction Method of Multipliers) on the primal objective function. More...
 
double solveWith (DualAMAType &dama, double *v, double *r, const bool staticProblem=false) const
 AMA (Alternating Minimization Algorithm) on the dual objective function. . More...
 

Public Attributes

MType M
 M – mass matrix.
 
bogus::SparseBlockMatrix
< Eigen::Matrix< double,
Dimension, Dimension > > 		E
 E – local rotation matrix ( contact basis coordinates to world coordinates )
 
HType H
 H – deformation gradient 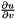$ \frac{\partial u}{\partial v} $ ( generalized coordinates <-> contact basis coordinates )
 
const double * f
 External forces.
 
const double * w
 Free velocity in world coordinates ( such that u = Hv + E^T w )
 
const double * mu
 Coulomb friction coefficients.
 
MInvType MInv
 

Detailed Description

template<unsigned Dimension>
struct bogus::PrimalFrictionProblem< Dimension >

Primal Coulomb friction problem for a block-diagonal mass matrix M with dense blocks.

\[ \left\{ \begin{array}{rcl} M v &=& H^T r - f \\ u &=& H v + E^T w \\ &s.t.& law (x,y) \end{array} \right. \]

where law is either SOCLaw (meaning solving a SOCQP) or CoulombLaw, and v are the velocities, r the contact forces and u the relative velocities at contact points. E is a rotation matrix transforming local contact basis coordinates into world coordinates , is is only useful for consistency with legacy interface.

Useful for solving friction problems in discrete systems with reduced coordinate models. Solving may be performed directly on this formulation, or on the dual formulation by constructing a DualFrictionProblem from this object. See also Constrained Iterative Solvers .

Member Function Documentation

template<unsigned Dimension>
void bogus::PrimalFrictionProblem< Dimension >::computeMInv ( )

Computes MInv from M. Required to build a DualFrictionProblem for the PrimalFrictionProblem, or to use the ADMM and matrix-free Gauss-Seidel solvers.

template<unsigned Dimension>
double bogus::PrimalFrictionProblem< Dimension >::solveWith ( ProductGaussSeidelType &  pgs,
double *  r,
const bool  staticProblem = false 
) const

Matrix-free Gauss-Seidel solver.

Note
Requires the computation of a factorization of M with computeMInv()
Parameters
rResulting forces and initial guess (in contact basis coordinates)
staticProblemIf true, solve this problem as a SOCQP instead of a Coulomb Friction problem
template<unsigned Dimension>
double bogus::PrimalFrictionProblem< Dimension >::solveWith ( ADMMType &  admm,
double  lambda,
double *  v,
double *  r 
) const

ADMM (Alternating Direction Method of Multipliers) on the primal objective function.

May only be used to solve SOCQP (static problems), not Coulomb friction problems

Parameters
lambdaproximal coefficient of the quadratic part (lambda = 0 means AMA)
vResulting velocities and initial guess
rResulting forces and initial guess (in contact basis coordinates)
Note
Requires the computation of a factorization of M with computeMInv()
template<unsigned Dimension>
double bogus::PrimalFrictionProblem< Dimension >::solveWith ( DualAMAType &  dama,
double *  v,
double *  r,
const bool  staticProblem = false 
) const

AMA (Alternating Minimization Algorithm) on the dual objective function. .

Does not require a factorization of M

Parameters
vResulting velocities and initial guess
rResulting forces and initial guess (in contact basis coordinates)
staticProblemIf true, solve this problem as a SOCQP instead of a Coulomb Friction problem
The documentation for this struct was generated from the following files: